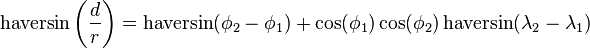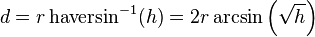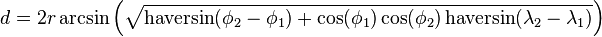2012. 10. 15. 19:17ㆍTips
How calculate the shortest distance between two points over the sphere?
구(Sphere) 위에서 최단 거리를 구하려면?
지구는 둥그니까...
우리가 보는 편면 지도 상에서의
두 지점을 직선으로 잇는 것은,
실제 지구상 최단거리는 아니다.
그래서 이에 대해서 정리한 것이
Haversine Formula다.
Haversine Formula에 대해서는
아래 예시 밑 단에 첨부한다.
Reference(From Wikipedia.org)
'Haversine Formula'
The haversine formula
For any two points on a sphere, the haversine of the central angle between them is given by
where
- haversin is the haversine function:
- d is the distance between the two points (along a great circle of the sphere; see spherical distance),
- r is the radius of the sphere,
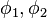 : latitude of point 1 and latitude of point 2
: latitude of point 1 and latitude of point 2 : longitude of point 1 and longitude of point 2
: longitude of point 1 and longitude of point 2
On the left side of the equals sign d/r is the central angle, assuming angles are measured in in radians (note that φ and &lambda can be converted from degrees to radians by multiplying by π/180 as usual).
Solve for d by applying the inverse haversine (if available) or by using the arcsine (inverse sine) function:
where h is haversin(d/r), or more explicitly:
'Tips' 카테고리의 다른 글
| 항공기 좋은 좌석을 검색한다. Seatguru! Search the seat for flying. (2) | 2012.10.29 |
|---|---|
| 추석 연휴, 저렴하게 영화보기. 신촌 아트레온 이벤트 (0) | 2012.09.25 |
| About Trans-Fat ; 트렌스지방산에 대하여 (0) | 2012.09.23 |